Unveiling Euler's Identity: Why This Equation is Called Mathematics' Most Beautiful

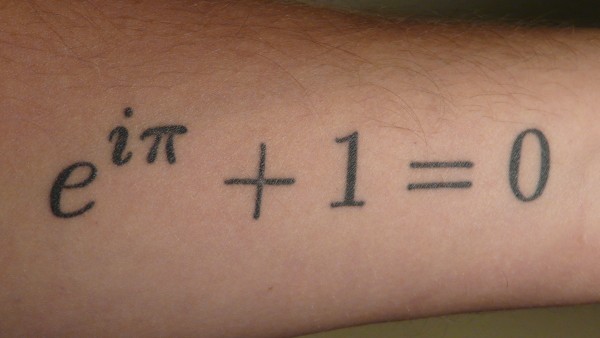
Euler's Identity: The Epitome of Mathematical Elegance

Among the intricate theories and complex calculations of mathematics, one equation stands out for its profound simplicity and astonishing comprehensiveness, widely celebrated as the 'most beautiful' ever discovered. This masterpiece is Euler's Identity, often written as:

$$e^{i\pi }+1=0$$

At first glance, its simplicity might belie its depth, but upon closer inspection, its elegance emerges from the harmonious convergence of five of the most fundamental constants in mathematics, united by three core operations.

The Five Pillars of Euler's Identity:

1. e (Euler's Number): Approximately 2.71828, this is the base of the natural logarithm. It arises naturally in processes of continuous growth and decay, appearing in calculus, compound interest, and probability.

2. i (The Imaginary Unit): Defined as the square root of -1 (−1​), i is the cornerstone of complex numbers. Its introduction expanded the realm of numbers beyond the real line, allowing solutions to equations that were previously considered impossible.

3. π (Pi): Approximately 3.14159, π is the ratio of a circle's circumference to its diameter. It is fundamental to geometry, trigonometry, and appears in countless areas of physics and engineering.

4. 1 (The Multiplicative Identity): The simplest positive integer, 1 is the identity element for multiplication; any number multiplied by 1 remains unchanged. It represents unity and existence.

5. 0 (The Additive Identity): The additive identity, 0 signifies nothingness or the absence of quantity. Any number added to 0 remains unchanged. It is crucial for arithmetic and algebra, serving as the origin on the number line.

The Three Fundamental Operations:

Euler's Identity masterfully weaves these constants together using the most basic mathematical operations:

1. Addition (+): The act of combining quantities.

2. Multiplication (implied in iπ): The repeated addition of a quantity.

3. Exponentiation (e.g., eiπ): The repeated multiplication of a base number by itself.

Why is it Considered Beautiful?

The profound beauty of Euler's Identity lies in several aspects:

• Unification: It brings together seemingly disparate branches of mathematics – arithmetic (0, 1), algebra (i), geometry (π), and analysis (e) – into a single, concise expression.

• Simplicity: Despite the complexity of the concepts it represents, the equation itself is remarkably simple, containing only five constants and three operations.

• Profound Connection: The equation elicits a sense of wonder: How can the base of natural logarithms, raised to an imaginary power of pi, precisely equal -1? This unexpected link reveals a deep, underlying harmony.

• Fundamental Nature: Each constant and operation in the equation is fundamental to its respective field, making their connection deeply significant.

• Elegance: Like a perfect poem or minimalist art, it contains no extraneous elements, presenting a pure, distilled mathematical truth.

To truly appreciate its beauty, it's helpful to understand its origin. Euler's Identity is a direct consequence of Euler's Formula ($e^{ix}=\cos x+i\sin x$), where setting $x=\pi$ leads to $e^{i\pi }=\cos \pi +i\sin \pi$. Since $\cos \pi =-1$ and $\sin \pi =0$, the formula simplifies to $e^{i\pi }=-1$, which then rearranges to $e^{i\pi }+1=0$.

This equation is not just a curiosity; it's a profound statement about the interconnectedness of mathematical concepts, revealing a hidden harmony that underpins the structure of the universe itself. It stands as a testament to the power and elegance of mathematical thought.